Quantum Networks

Transfer of entanglements (Entanglement Swapping)

The big problem in generating entangled pairs over a link is the increasing “state decay” with increasing distance of the nodes; due to the no-cloning theorem it is also not possible to amplify the signal in between. Thus, it is not directly possible to stably distribute entangled pairs (including Bell pairs) over arbitrarily large distances.

To make this possible, however, entanglement swapping was developed, i.e. the transfer and concatenation of entanglements.

A Bell pair between two end nodes of the quantum network, i.e., a quantum E2E link, can be created by a continuous combined generation (stringing together) of Bell pairs along the link sections (with intermediate nodes). Each intermediate node along the path can link the two adjacent QuBit pairs (right/left side) and thus create a new entanglement between the QuBits on its two neighboring nodes.

This process of entanglement transfer proceeds as follows: In the upper part of the figure, nodes A and B originally share the (unknown) entangled QuBit pair-(X1,X2) and nodes B and C share the entangled QuBit pair-(Y1,Y2). But the goal is to achieve the entanglement of a QuBit pair between nodes A and C. To achieve this goal, the QuBit-X2 is teleported to node-C, for which the QuBit-pair-(Y1,Y2) is used. For this purpose, node-B makes a Bell measurement on QuBits X2 and Y1, which destroys the entanglement between QuBit-pair-(Y1,Y2). Instead, QuBit-X2 is teleported to node-C with the Bell measurement and the bits for the Pauli correction and “re-generated” in QuBit-Y2, where QuBit-X2=Y2 is/remains still entangled with QuBit-X1. QuBits X1 and X2=Y2 are still unknown. The figure shows the result in the lower part.

Initial state: Three nodes A,B,C with two interleaved QuBit pairs

Final state: QuBit Y2 assumes state X2 and is entangled with X1

Figure: Swapping process

In addition, the two bits of the Bell measurement process in node B still have to be transported further, since they contain information about the Bell measurement pair (X2, Y1). Quantum nodes that generate remote entangled pairs via entanglement swapping are called quantum repeaters.

The genesis of entanglement

The problem of quantum connectivity is closely related to the generation (and distribution) of Bell pairs. So how are Bell pairs generated and brought to the endpoints? In a quantum network, the entanglement is generated locally; subsequently, the displacement of one or both entangled QuBits to their destinations takes place within the framework of quantum channels.

Photons are a good “raw material” for this purpose: they have rather little interaction with the environment (i.e., a low tendency to decoherence), they can be processed with many standard optical components, and the transmission takes place at high speed (speed of light) and with little loss. However, photons cannot be stored; their flying QuBit state (flying QuBit) must therefore be transferred to a matter QuBit (e.g., an electron spin or an atomic state) for further processing using transducers.

This transmission process is not error-free and it must be possible to clearly distinguish the final state between successful and unsuccessful. Entanglement productions that can distinguish between successful and unsuccessful are called “Heralded Entanglement Generation Schemes”.

There are three basic schemes for creating heralded entanglements between two quantum nodes:

• Midpoint scheme: The source of the entangled QuBit-pair-(X1,X2) sends an entangled photon pair via Qu-channels to the two target nodes A and B. The source of the entangled QuBit-pair-(X1,X2) sends an entangled photon pair via Qu-channels to the two target nodes A and B. There, transducers transfer the entanglement from the photon QuBit pair-(X1,X2) (flying QuBits) to a matter QuBit pair-(Y1,Y2), respectively. The transducers have knowledge about the success/failure of the process and can report this back via classical data channels.

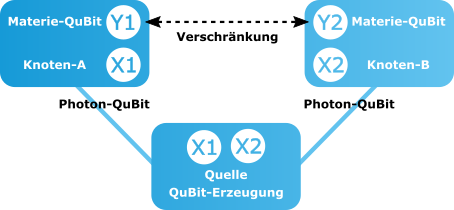Figure: Midpoint scheme for generating heralded entanglements.

• Source scheme: A source node-A sends a flying QuBit-X1, which is entangled with a local matter QuBit-Y1, to destination node-B. There, a transducer transmits the entanglement to a matter QuBit-Y2 and can in turn report back the success/failure.

Figure: Source scheme for generating heralded entanglements.

• Double-ended scheme: Two source nodes A and B send flying QuBits (X1,X2), which are locally entangled with matter QuBits (Y1,Y2). The flying-QuBits-(X1,X2) are not yet entangled with each other for the time being. A detector somewhere between the two source nodes A and B makes a joint Bell measurement on both Flying-QuBits-(X1,X2), which transfers them and thus also the distant Matter-QuBits-(Y1,Y2) in the two source locations A and B into a joint entangled state (always only with probability <1). In this scheme, the detector “knows” about the success/failure and sends a corresponding message back to the source locations A and B via classical channels.

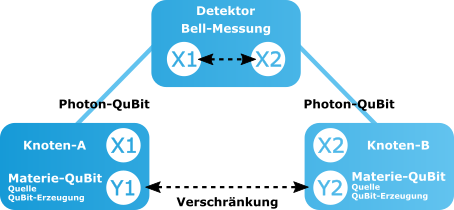Figure: Double-ended scheme for generating heralded entanglements.

The midpoint scheme is so far more robust to photon loss; in the other two schemes, nodes have more control over entangled pair generation for this. This offers much room for different technological developments.

Dr. Peter Kaufmann (DFN)

Version: 06.12.2021