Quantum Key Distribution
Quantum Key Distribution

To generate secure keys for message transmission, random numbers can be generated using quantum mechanics. Quantum Key Distribution (QKD) is part of the field of Quantum Cryptograpy.
The advantage of this communication method is that, thanks to the No-Cloning-Theorem, these states cannot be copied in any way, since a measurement would always destroy the previous state and therefore an eavesdropping would be noticed. This encryption method will therefore also be tap-proofed in the future in view of quantum computing.
Protocols
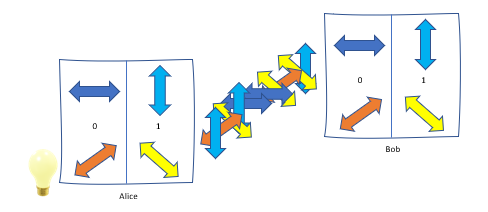
The common protocols presented are based on discrete quantum properties of photons, such as the polarization states that represent different QuBits: vertical (+-base) or diagonal (x-base) oscillation directions correspond to a 0 and horizontal (+-base) or anti-diagonal (x-base ) Polarizations to a 1. If a vertical polarization is measured with a x-base, the measurement result is not clear, instead one receives an (anti-)diagonal polarization with 50% probability each. This is often the case because in the following protocols the choice of base will be random.
BB84 (Bennett und Brassard 1984)
This protocol is one of the first methods used for quantum communication. It is one of the Prepare-and-Measure (PM) protocols because unentangled states are first prepared and then measured.
- Alice generates random bit sequences of zeros and ones
- Alice generates random bases (+ or x)
- Alice sends the resulting polarisation states of photons to Bob
- Bob measures recieved photons with random bases
- Bob has received bit sequence available
This is followed by a public discussion of the received photons along a classical communication channel.
- Bob reports to Alice which bases he used for decoding
- Alice is responding if they were correct
Thus now Alice and Bob have some matching bits. However, some additional bits must now be disclosed in order to check whether they match or have been compromised by an eavesdropper. If the error rate is small enough, it can be assumed that no one was listening to the channel.
- Bob discloses some random bit keys
- Alice confirmes their authenticity
At the end the previously disclosed key bits have to be removed from the remaining secret bits. Classical error correction algorithm assure Alice and Bob receiving the same key from the remaining common random numbers.
E91 (Ekert 1991)
Entanglement-based (EB) protocols exploit quantum entanglement. Two entangled particles have a common state and even if the two are at different locations, a consistent state can be measured. Photon pairs with maximum entanglement are also called Bell pairs. Quantum states are generally very fragile and do not last forever. This particularly applies to entanglement. It is destroyed after a few hundred kilometers due to natural influences when spreading through glass fibers or open space.
To generate entangled quantum pairs parametric fluorescence is mainly used. Here, two photons with correlated polarization are generated when light passes through a doped crystal.
After receiving the photons via a classic channel, also here it is clarified whether a common basis was used in the measurement. A correlation function is used to calculate whether the channel was influenced by eavesdroppers. Finally, the matching values with the same basis are processed again to form a common key.
Behavior in the event of possible eavesdropping attacks:
QKD is physically secure, but an insufficiently perfect implementation results in vulnerabilities, which are briefly outlined below.
- Man-in-the-Middle-Attack: remediable through authentification (e.g. through Pre-shared Secrets)
- Side channel attacks:
– Photon-Number-Splitting: One-Photon-Source difficult to realize -> additionally generated photons are intercepted by the eavesdropper without the notice of the other participants, so that parts of the key become known to the attacker -> introduce Decoy-States (e.g. sending with different intensity in order to detect the attack; adjust timing if necessary)
– Trojan Horse: radiating a high pulse of light -> information about the quantum states can be obtained from reflections. Can be prevented with optical isolators or spectral filters.
(M)DI in particular offers fewer attack surfaces and is therefore more robust against side channel attacks. This means that the known attack methods in QKD can be successfully repelled.
DI (Device-Independent) vs. MDI (Measurement-Device-Independent)
DI protocols are intended to ensure the correct behavior of the devices during key generation (e.g. also in the case of side channel attacks) and thus offer independence from the devices used. This is ensured using entangled states and calculated correlation functions. Since the key is discarded whenever the correlation function of both quantum pairs does not behave as expected, this is reflected in reduced key rates and ranges. But these protocols are particularly secure.
In contrast to DI, with MDI the measurements are taking place at a central relay. Before the measurement interference takes place at the relay. The measurement result from the central relay is made public, however this can only be decoded together with the knowledge of the previously prepared state and so a secret key can be obtained. A very promising process is the so-called Twin-Field procedure. Overall, these methods lead to a greater range and higher transmission rates.
Comparison to PQC (Post-Quantum Cryptography):
While the security of QKD is based on the physics of quantum mechanics, in PQC it only depends on the complexity of algorithms that are mathematically difficult to calculate. These methods should still be safe as quantum computers continue to develop.
A detailed comparison of the features of QKD versus PQC can be found in the document WiN-Lab Research: PQC versus QKD.
For further informations see Tutorials on Quantum Communications in german language.
Version: 02.08.2024
