Quantenteleportation
Quantenteleportation
Die Quantenteleportation mittels Quantengattern ist in den folgenden Skizzen schematisch bzw. als Schaltplan bestehend aus CNOT, Hadamard und XZ Gattern dargestellt [1,2]:
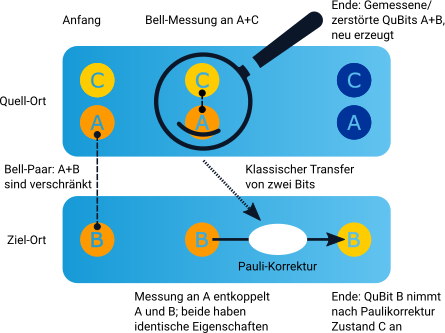
Ziel der Quantenteleportation ist es, den Zustand des QuBits C auf ein anderes QuBit B zu übertragen. Aufgrund des No-Cloning Theorem ist es aber nicht möglich den Zustand eines QuBits C direkt auf ein anderes zu übertragen, ohne dabei den Zustand von QuBit C zu ändern. Der Zustand des QuBits C ist anfangs |QC>:
\Ket{Q_C} = \alpha\Ket{0} + \beta\Ket{1}Zur Durchführung der Quantenteleportation sind drei QuBits nötig: Das QuBit C hat den zu übertragenden Zustand, die beiden anderen miteinander verschränkten QuBits (A und B) dienen zur Übertragung des Zustands von QuBit C auf QuBit B.
Ablauf einer Quantenteleportation
- Es werden zwei QuBits A und B miteinander verschränkt. Während Bob QuBit B behält, sendet er QuBit A zu Alice.
- Alice verknüpft ihr QuBit C mit dem empfangenen QuBit A über ein CNOT Gatter und wendet ein Hadamard Gatter an.
- Alice misst den Zustand der QuBits C und A.
- Alice teilt das Ergebnis der Messungen -zwei klassische Bits- über einen klassischen Kommunikationskanal mit.
- Je nach Messergebnis wendet Bob an seinem QuBit B X und/oder Z Gatter an, sodass sein QuBit B am Ende den gleichen Zustand hat wie QuBit C am Anfang des Teleportationsprozesses.
Mathematische Beschreibung von Schritt 1
Die Verschränkung von QuBit A und B ergibt:
\Ket{e} = \frac{1}{\sqrt{2}}(\Ket{00} + \Ket{11}) = \frac{1}{\sqrt{2}}(\Ket{0}_{A}\Ket{0}_{B}+\Ket{1}_{A}\Ket{1}_{B})Damit ergibt sich, zusammen mit QuBit C dessen Einteilchenzustand übertragen werden soll, folgender Zustandsvektor für den Gesamtzustand bei 1.:
\Ket{Q_C} \otimes \Ket{e} = \frac{1}{\sqrt{2}}(\alpha\Ket{000} + \alpha\Ket{011} + \beta\Ket{100} + \beta\Ket{111})Exkurs: Verknüpfung von Gattern zur Beschreibung der Evolution des Gesamtsystems
Um einen mathematischen Ausdruck zur Beschreibung der Evolution des Gesamtsystems ausgehend von den bisher beschriebenen Quantengattern zu erhalten, wird hier zuerst der Fall von einem System aus zwei QuBits betrachtet. Während an QuBit q0 keine Operation durchgeführt wird, wirkt auf QuBit q1 ein Hadamard Gatter [3]:
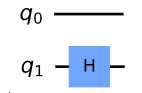
Das Ausführen keines Gatters lässt QuBit q0 unverändert und wird deshalb durch die Identitätsmatrix I beschrieben:
I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}
Die Matrix G, die den Zustandsvektor der beiden QuBits entsprechend der Schaltung verändert, folgt über ein Tensorprodukt der Matrizen I und H:
G = I \otimes H = \begin{bmatrix} H & 0 \\ 0 & H \end{bmatrix} = \frac{1}{\sqrt{2}} \Biggl[ \begin{bmatrix} 1 & 1 & 0 & 0 \\ 1 & -1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & -1 \end{bmatrix} \Biggr]
Für die verwendete Anordnung der Einträge im Zustandsvektor erhält man also G indem man die Matrizen im Schaltplan von oben nach unten abliest und dann von links nach rechts über das Tensorprodukt verknüpft.
Mathematische Beschreibung von Schritt 2 und Erläuterung der Schritte 3 und 4
Analog zum obigen Fall mit den QuBits q0 und q1 wird die Verknüpfung der QuBits C und A durch ein CNOT Gatter über ein Tensorprodukt der Matrizen CNOT und I erhalten:
G_1 = CNOT \otimes I = \Biggl[ \begin{bmatrix} I & 0 & 0 & 0 \\ 0 & I & 0 & 0 \\ 0 & 0 & 0 & I \\ 0 & 0 & I & 0 \end{bmatrix} \Biggr]
Die Beschreibung der nachfolgenden Anwendung eines Hadamard Gatters auf QuBit C folgt über das Tensorprodukt der Matrizen H, I und I:
G_2 = H \otimes I \otimes I = \frac{1}{\sqrt{2}} \Biggl[ \begin{bmatrix} I & 0 & I & 0 \\ 0 & I & 0 & I \\ I & 0 & -I & 0 \\ 0 & I & 0 & -I \end{bmatrix} \Biggr]
Über die Anwendung von G2G1 (normales Matrixprodukt!) auf den Zustandsvektor für den Gesamtzustand bei 1. ergibt sich dann der Zustandsvektor für den Gesamtzustand bei 2.:
(G_2 \cdot G_1) (\Ket{Q_C} \otimes \Ket{e}) = \\ \frac{1}{\sqrt{2}} (H \otimes I \otimes I) \cdot (CNOT \otimes I) (\alpha\Ket{000}+\alpha\Ket{011}+\beta\Ket{100} + \beta\Ket{111}) = \\ \frac{1}{\sqrt{2}} (H \otimes I \otimes I) (\alpha\Ket{000} + \alpha\Ket{011} + \beta\Ket{101} + \beta\Ket{110}) = \\ \frac{1}{2}(\alpha(\Ket{000} + \Ket{011} + \Ket{100} + \Ket{111}) + \beta(\Ket{001} + \Ket{010} - \Ket{101} - \Ket{110})) = \\ \frac{1}{2}(\color{green}{\Ket{00}}\color{black}{(}\color{blue}{\alpha\Ket{0} + \beta\Ket{1}}\color{black}{)+} \color{green}{\Ket{01}}\color{black}{(}\color{blue}{\alpha\Ket{1} + \beta\Ket{0}}\color{black}{)+}\color{green}{\Ket{10}}\color{black}{(}\color{blue}{\alpha\Ket{0}-\beta\Ket{1}}\color{black}{)+}\color{green}{\Ket{11}}\color{black}{(}\color{blue}{\alpha\Ket{1} - \beta\Ket{0}}\color{black}{))}
Als nächstes führt Alice jeweils eine Messung an ihren beiden QuBits C und A durch. Nach den Messungen hat sie mit gleicher Wahrscheinlichkeit (25%) einen der vier grün markierten Zustände in der obigen Gleichung. Alice sendet das Messergebnis codiert in zwei klassische Bits an Bob, dessen QuBit B durch die Messungen den jeweiligen blau markierten Zustand angenommen hat:
| Messergebnis C, A (Alice) | Zustand QuBits |QC QA> nach Messung (Alice) | Zustand QuBit |QB> nach Messung (Bob) |
| 0,0 | |00〉 | α|0〉+β|1〉 |
| 0,1 | |01〉 | α|1〉+β|0〉 |
| 1,0 | |10〉 | α|0〉-β|1〉 |
| 1,1 | |11〉 | α|1〉-β|0〉 |
Schritt 5: X und Z Gatter
Nur für das Messergebnis 0,0 hat Bobs QuBit B direkt den ursprünglichen Zustand des zu übertragenden QuBits C. Für die drei anderen möglichen Messergebnisse ist eine Anpassung des Zustandes von QuBit B erforderlich. Hierfür werden die sogenannte X und Z Gatter verwendet:
Das X Gatter invertiert den Zustand von |0〉 zu |1〉 und umgekehrt [1]:
Das Z Gatter führt zu einer Änderung des Zustands |+〉 zu |-〉 bzw. |-〉 zu |+〉 [1]:
Durch Verwendung dieser Gatter kann Bob sein QuBit B in den ursprünglichen Zustand von QuBit C bringen. Nachfolgende Tabelle zeigt welche Gatter Bob auf sein QuBit B abhängig von dem Messergebnis anwenden muss:
| Messergebnis C, A (Alice) | erforderliches Gatter für QuBit B (Bob) |
| 0,0 | keine |
| 0,1 | X |
| 1,0 | Z |
| 1,1 | ZX |
Exkurs: Mathematische Darstellung der X und Z Gatter
Das X Gatter ist eine simple 2×2 Matrix. In diesem Beispiel ändert das X Gatter den QuBit Zustand |0〉 zu |1〉:
X = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix},\Ket{0} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, X\Ket{0} = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}
Auch beim Z Gatter handelt es sich um eine einfache 2×2 Matrix. Gezeigt wird die Änderung von |+> zu |->:
Z = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}, \Ket{+} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \end{bmatrix}, Z \Ket{+} = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ -1 \end{bmatrix} = \Ket{-}
Quellen
[1] M. Ellerhoff. Mit Quanten Rechnen. ISBN 978-3-658-31221-3
[2] P. Kaufmann, S. Naegele-Jackson. II. Quantenrevolution – die Welt der Qubits. In: DFN Mitteilungen Ausgabe 99, Juni 2021
[3] ibm. Qiskit Textbook. https://github.com/qiskit-community/qiskit-textbook
Stand: 18.06.2024
